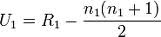29/03/2012
CASOS AJUSTADOS MAYORES A 15. para este tipo de casos, dentro de la prueba de Wilcoxon se debe obtener la diferencia de rangos por medio de las tres formulas que me permitan obtener los valores de NTmas, sigmaT mas y el valor de Z al final, a partir del cual se aplicara la decision estadistica para saber si la hipotesis nula se rechaza o se acepta..
Es importante recordar que cuando se especifique que se debe trabajar con dos colas, el valor de alfa debe ser dividido entre dos, si solo se trabaja con una cola, el calor de alfa sera el mismo, es decir, que no cambiara.
Al momento de tomar la decision estadistica, se procedera de la siguiente manera:
Si el valor de Z es mayor o igual al valor absoluto, la Ho se rechaza.
Es importante señalar tambien que la prueba de Wilcoxon se utiliza para diferencias proporcionales.
Si n es menor que 15 entonces hay que considerar el valor de alfa, si este es con una cola o con dos colas, porteriormente se obtiene una valor, el cual sera restado al valor que se obtenga de la tabla dos en sonde se toma en cuenta el valor de N corregido y el valor real de alfa. Lo que nos da como resultado un intervalo, al que realizaremos una operacion de resta, y al resultado obtenido le dividiremos entre el valor obtenido de la primer tabla en la que se considera si alfa trabaja con una cola o dos colas.
jueves, 29 de marzo de 2012
martes, 27 de marzo de 2012
27/03/2012
EL APRENDIZAJE SIGNIFICATIVO PARA MI EL DÍA DE HOY FUÉ SOBRE LA PRUEBA DE WILCONXON PARA OBTENER LA DIFERENCIA DE RANGOS.
CUANDO SE TIENE EL VALOR DE ALFA, Y SE LLEGA AL PASO 5 PARA ENCONTRAR EL VALOR DE PROBABILIDAD, SE DEBE TENER COMO BASE LA TABLA QUE NOS SIRVE PARA ESTE CASO, LA CUAL ES LLAMADA VALOR DE PROBABILIDAD ASOCIADO A Tmas.
EL PRIMER PASO PARA OBTENER EL VALOR DE PROBABILIDAD ES OBTENER LOS SIGUIENTES VALORES:
n= TAMAÑO DE LA MUESTRA
N= VALOR DE N CORREGIDO
Y EL VALOR DE ALFA
UNA VEZ QUE SE OBTIENEN ESTOS VALORES, DEBO TOMAR MI PRIMER TABLA EN LA QUE UBICARÉ EL TAMAÑO DE MI POBLACIÓN, PRIMERO, Y POSTERIORMENTE DIVIDIRE ENTRE DOS EL VALOR DE ALFA, ENCONTRANDO ASI LA UNIÓN ENTRE ESTOS DOS . Y ASÍ OBTENDRE UN PRIMER VALOR.
POSTERIORMENTE ME VOY A LA SEGUNDA TABLA Y UBICARÉ EN ESTA EL VALOR DE n CORREGIDA, ENCONTRANDO EL RESULTADO EN EL QUE SE UNA CON EL PORCENTAJE DE CONFIABILIDAD, LO CUAL ME DARÁ COMO RESULTADO UN INTERVALO, QUE SE EXPRESA A MANERA DE RESTA, REALIZARÉ LA OPERACIÓN Y EL RESULTADO OBTENIDO LO DIVIDIRÉ ENTRE EL VALOR QUE OBTUVE, ESTE SERÁ MI VALOR DE PROBABILIDAD, TAMBIÉN LLAMADO T (mas).
ES POSIBLE ENCONTRAR UN TIPO DE GRÁFICA COMO LA SIGUIENTE:
EL APRENDIZAJE SIGNIFICATIVO PARA MI EL DÍA DE HOY FUÉ SOBRE LA PRUEBA DE WILCONXON PARA OBTENER LA DIFERENCIA DE RANGOS.
CUANDO SE TIENE EL VALOR DE ALFA, Y SE LLEGA AL PASO 5 PARA ENCONTRAR EL VALOR DE PROBABILIDAD, SE DEBE TENER COMO BASE LA TABLA QUE NOS SIRVE PARA ESTE CASO, LA CUAL ES LLAMADA VALOR DE PROBABILIDAD ASOCIADO A Tmas.
EL PRIMER PASO PARA OBTENER EL VALOR DE PROBABILIDAD ES OBTENER LOS SIGUIENTES VALORES:
n= TAMAÑO DE LA MUESTRA
N= VALOR DE N CORREGIDO
Y EL VALOR DE ALFA
UNA VEZ QUE SE OBTIENEN ESTOS VALORES, DEBO TOMAR MI PRIMER TABLA EN LA QUE UBICARÉ EL TAMAÑO DE MI POBLACIÓN, PRIMERO, Y POSTERIORMENTE DIVIDIRE ENTRE DOS EL VALOR DE ALFA, ENCONTRANDO ASI LA UNIÓN ENTRE ESTOS DOS . Y ASÍ OBTENDRE UN PRIMER VALOR.
POSTERIORMENTE ME VOY A LA SEGUNDA TABLA Y UBICARÉ EN ESTA EL VALOR DE n CORREGIDA, ENCONTRANDO EL RESULTADO EN EL QUE SE UNA CON EL PORCENTAJE DE CONFIABILIDAD, LO CUAL ME DARÁ COMO RESULTADO UN INTERVALO, QUE SE EXPRESA A MANERA DE RESTA, REALIZARÉ LA OPERACIÓN Y EL RESULTADO OBTENIDO LO DIVIDIRÉ ENTRE EL VALOR QUE OBTUVE, ESTE SERÁ MI VALOR DE PROBABILIDAD, TAMBIÉN LLAMADO T (mas).
ES POSIBLE ENCONTRAR UN TIPO DE GRÁFICA COMO LA SIGUIENTE:
viernes, 23 de marzo de 2012
23/03/2012
El día de hoy trabajamos con la prueba de Wilcoxon, la cual es una prueba de rangos asignados, que por no pertenecer a las pruebas NO PARAMËTRICAS, no requiiere de una distribución específica.
Se utiliza para comparar dos grupos relacionados de rangos, y para comparar que la diferencia sea estadísticamente significativa..
Los pasos a seguir para aplicar esta prueba son los siguientes:
1.-OBTENER LA DIFERENCIA DE RANGOS
2.-SELECCIONAR LOS RANGOS POSITIVOS Y LOS NEGATIVOS
3.-NUMERAR LOS RANGOS POSITIVOS Y LOS NEGATIVOS, Solo numerarlos no se deben ordenar
4.- OBTENER EL VALOR DE T mas y T menos.. Esto es el total de lugares que ocupan los valores positivos y los negativos.
5.-ENCONTRAR EL VALOR DE PROBABILIDAD SOCIADO A T(mas), CON EL NÚMERO AJUSTADO DE DATOS
6.- DECISIÓN ESTADÍSTICA
ALGUNAS DE LAS FÓRMULAS USADAS EN ESTA PRUEBA SON:
El día de hoy trabajamos con la prueba de Wilcoxon, la cual es una prueba de rangos asignados, que por no pertenecer a las pruebas NO PARAMËTRICAS, no requiiere de una distribución específica.
Se utiliza para comparar dos grupos relacionados de rangos, y para comparar que la diferencia sea estadísticamente significativa..
Los pasos a seguir para aplicar esta prueba son los siguientes:
1.-OBTENER LA DIFERENCIA DE RANGOS
2.-SELECCIONAR LOS RANGOS POSITIVOS Y LOS NEGATIVOS
3.-NUMERAR LOS RANGOS POSITIVOS Y LOS NEGATIVOS, Solo numerarlos no se deben ordenar
4.- OBTENER EL VALOR DE T mas y T menos.. Esto es el total de lugares que ocupan los valores positivos y los negativos.
5.-ENCONTRAR EL VALOR DE PROBABILIDAD SOCIADO A T(mas), CON EL NÚMERO AJUSTADO DE DATOS
6.- DECISIÓN ESTADÍSTICA
ALGUNAS DE LAS FÓRMULAS USADAS EN ESTA PRUEBA SON:
22/03/2012
El día de hoy se aplico la fórmula para la prueba de Sperman la cual como recordaremos es la siguiente:
Mediante el uso de esta formula sabremos si la correlacion existente entre las variables es baja o nula, media o moderada, u alta o grave.
Se debe proceder de la manera siguiente conforme a los pasos presentados a continuacion para aplicar dicha fórmula:
1.- Las variables deben ser ordenadas
2.- Una vez ordenadas las variables, se procede a obtener la prueba de diferencia de rangos.
3.- Construir una tabla de diferencia de rangos.
4.- En dado caso que las variables se empaten se debe aplicar la fórmula específicada para esto.
5.- Interpretacion de los datos.
Para los datos empatados se puede proceder de la sig. manera:
De las tablas que se elaboran, se debe obtener el cuadrado de la diferencia de cada uno de los lugares que ocupan las filas.
El día de hoy se aplico la fórmula para la prueba de Sperman la cual como recordaremos es la siguiente:
Mediante el uso de esta formula sabremos si la correlacion existente entre las variables es baja o nula, media o moderada, u alta o grave.
Se debe proceder de la manera siguiente conforme a los pasos presentados a continuacion para aplicar dicha fórmula:
1.- Las variables deben ser ordenadas
2.- Una vez ordenadas las variables, se procede a obtener la prueba de diferencia de rangos.
3.- Construir una tabla de diferencia de rangos.
4.- En dado caso que las variables se empaten se debe aplicar la fórmula específicada para esto.
5.- Interpretacion de los datos.
Para los datos empatados se puede proceder de la sig. manera:
De las tablas que se elaboran, se debe obtener el cuadrado de la diferencia de cada uno de los lugares que ocupan las filas.
martes, 20 de marzo de 2012
20/03/2012
PRUEBA DE CORRELACIÓN DE SPEARMAN o PRUEBAS DE LIBRE DISTRIBUCIÓN
Esta prueba es una alternativa al coeficiente de correlación lineal y a la correspondiente prueba "T", la única condición que exige este método es que las variables sean por lo menos ORDINALES, es decir que se puedan ordenar.
Es importante señalar que dentro de la prueba de SPEARMAN, no es posible trabajar con variables nominales, esto debido a que no es posible ordenarlas.
por ejemplo:
Al trabajar con categorias como la edad, el nivel de estudios, el peso, la estatura, etc, es posoble aplicar esta prueba, ya que todas estas variables pueden ser ordenadas jerarquicamente.
En cambio al trabajar con variables nominales como el sexo, color favorito, etc, no es posible usar esta prueba, ya que las variables no llevan un orden.
Es importante mencionar que en esta prueba los datos no se encuentran distrubuidos normalmente, sino que son dispersos, en una gráfica quedarían representados más o menos así
La fórmula que se utiliza en esta prueba es la siguiente:
PRUEBA DE CORRELACIÓN DE SPEARMAN o PRUEBAS DE LIBRE DISTRIBUCIÓN
Esta prueba es una alternativa al coeficiente de correlación lineal y a la correspondiente prueba "T", la única condición que exige este método es que las variables sean por lo menos ORDINALES, es decir que se puedan ordenar.
Es importante señalar que dentro de la prueba de SPEARMAN, no es posible trabajar con variables nominales, esto debido a que no es posible ordenarlas.
por ejemplo:
Al trabajar con categorias como la edad, el nivel de estudios, el peso, la estatura, etc, es posoble aplicar esta prueba, ya que todas estas variables pueden ser ordenadas jerarquicamente.
En cambio al trabajar con variables nominales como el sexo, color favorito, etc, no es posible usar esta prueba, ya que las variables no llevan un orden.
Es importante mencionar que en esta prueba los datos no se encuentran distrubuidos normalmente, sino que son dispersos, en una gráfica quedarían representados más o menos así
La fórmula que se utiliza en esta prueba es la siguiente:
esta prueba nos permite obtener la PRUEBA DE DIFERENCIA DE RANGOS.
viernes, 16 de marzo de 2012
16/03/2012
PRUEBA DE HOMOGENEIDAD
Al interpretar mis datos con la prueba de homogeneidad, debo considerar que el proceso para determinar si rechazo o no mi Hinv. es el mismo que en la prueba de independencia, excepto que al señalar mis hipotesis en los tipos de caso, que son el CASO 1 y el CASO 2, se establece si hay homogeneidad o no la hay . Es decir:
CASO 1 Hinv. SI hay homogeneidad
Ho: NO hay homogeneidad
H1 : SI homogeneidad
CASO 2 Hinv: NO hay homogeneidad
Ho: SI hay homogeneidad
H1: NO hay homogeneidad
De lo que se determinarà que:
Si SI rechazo mi hipotesis de homogeneidad, SI habrà evidencia suficiente para sostener mi Hinv.
Por otra parte, si NO rechazo mi hipòtesis de homogeneidad, NO habrà evidencia suficiente para considerar mi Hinv.
Como podemos darnos cuenta, es en la interpretacion de los datos, donde mi HIPOTESIS CAMBIA, de nombrarse independiente, a nombrarse homogenea.
PRUEBA DE HOMOGENEIDAD
Al interpretar mis datos con la prueba de homogeneidad, debo considerar que el proceso para determinar si rechazo o no mi Hinv. es el mismo que en la prueba de independencia, excepto que al señalar mis hipotesis en los tipos de caso, que son el CASO 1 y el CASO 2, se establece si hay homogeneidad o no la hay . Es decir:
CASO 1 Hinv. SI hay homogeneidad
Ho: NO hay homogeneidad
H1 : SI homogeneidad
CASO 2 Hinv: NO hay homogeneidad
Ho: SI hay homogeneidad
H1: NO hay homogeneidad
De lo que se determinarà que:
Si SI rechazo mi hipotesis de homogeneidad, SI habrà evidencia suficiente para sostener mi Hinv.
Por otra parte, si NO rechazo mi hipòtesis de homogeneidad, NO habrà evidencia suficiente para considerar mi Hinv.
Como podemos darnos cuenta, es en la interpretacion de los datos, donde mi HIPOTESIS CAMBIA, de nombrarse independiente, a nombrarse homogenea.
jueves, 15 de marzo de 2012
15/03/2012
MI APRENDIZAJE el dìa de hoy surante el seminario de estadìstica aplicada a la investigaciòn educativa fue que la formula de YATES es muy ùtil y sencilla de usar, esto claro solo en los casos especiales en que se nos presenta una tabla con dos filas y con dos columnas.
De entrada parece una fòrmula complicada, por la extensiòn y sus componentes, pero al sustit6uir no es tan complicado como aparenta. Lo indispensable es sustituir bien las cantidades, y realizar las operaciones de manera adecuada para no caer en errores.
Por otra parte dio inicio el tema de PRUEBA DE HOMOGENEIDAD, la cual es una variante de la prueba de independencia, y se utiliza para comparar proporciones en las que ocurren los valores de una sola variable categòrica, en varias poblaciones distintas.
El procedimiento es el mismo que se aplica en la prueba de independencia, y se determinara que paso seguir para obtener el ESTADISTICO DE PRUEBA, dependiendo tambièn de cuantas filas y cuantas columnas tenemos.
MI APRENDIZAJE el dìa de hoy surante el seminario de estadìstica aplicada a la investigaciòn educativa fue que la formula de YATES es muy ùtil y sencilla de usar, esto claro solo en los casos especiales en que se nos presenta una tabla con dos filas y con dos columnas.
De entrada parece una fòrmula complicada, por la extensiòn y sus componentes, pero al sustit6uir no es tan complicado como aparenta. Lo indispensable es sustituir bien las cantidades, y realizar las operaciones de manera adecuada para no caer en errores.
Por otra parte dio inicio el tema de PRUEBA DE HOMOGENEIDAD, la cual es una variante de la prueba de independencia, y se utiliza para comparar proporciones en las que ocurren los valores de una sola variable categòrica, en varias poblaciones distintas.
El procedimiento es el mismo que se aplica en la prueba de independencia, y se determinara que paso seguir para obtener el ESTADISTICO DE PRUEBA, dependiendo tambièn de cuantas filas y cuantas columnas tenemos.
martes, 13 de marzo de 2012
13/03/2012
CORRECCIÓN DE YATES
Esta formula también es llamada CORREGIDA o SINTETIZADA, y es útil al encontrarnos con un caso especial en pruebas de independencia.
Estos casos especiales, se refieren a el encontrar una tabla que solo cuente con DOS FILAS, así como con DOS COLUMNAS, es decir, que al obtener los GRADOS DE LIBERTAD, estos nos den como resultado 1.
Un ejemplo de este tipo de tablas es la siguiente:
CON DÉFICIT DE ATENCIÓN SIN DÉFICIT DE ATENCIÓN TOTALES
M 33 112 145
H 53 201 254
TOTAL 86 313 399
LA FÓRMULA QUE DEBEMOS UTILIZAR LLAMADA CORRECCIÓN DE YATES es la sig:
En esta fórmula solo debemos sustituir los datos que se presentan en nuestra tabla. Donde n, representa el total de datos , que en el caso de nuestra tabla anterior es 399.
CORRECCIÓN DE YATES
Esta formula también es llamada CORREGIDA o SINTETIZADA, y es útil al encontrarnos con un caso especial en pruebas de independencia.
Estos casos especiales, se refieren a el encontrar una tabla que solo cuente con DOS FILAS, así como con DOS COLUMNAS, es decir, que al obtener los GRADOS DE LIBERTAD, estos nos den como resultado 1.
Un ejemplo de este tipo de tablas es la siguiente:
CON DÉFICIT DE ATENCIÓN SIN DÉFICIT DE ATENCIÓN TOTALES
M 33 112 145
H 53 201 254
TOTAL 86 313 399
LA FÓRMULA QUE DEBEMOS UTILIZAR LLAMADA CORRECCIÓN DE YATES es la sig:
En esta fórmula solo debemos sustituir los datos que se presentan en nuestra tabla. Donde n, representa el total de datos , que en el caso de nuestra tabla anterior es 399.
viernes, 9 de marzo de 2012
09/03/2012
Realizamos dos ejercicios durante la clase del seminario del dís de hoy, algo que no me quedo muy claro la sesión pasada fue el paso numéro 6, en el que identifico mi hipótesis independiente, ya que me resultaba confuso.
Lo que entendi el día de hoy acerca de este punto, es que debo saber cual de las dos hipótesis es la independiente, si la ALTERNATIVA o la NULA, mediante los sig. pasos:
CASO 1 Hinv: INDEPENDIENTE donde Ho: NO HAY INDEPENDENCIA
H1: SI HAY INDEPENDENCIA
CASO 2 Hinv: NO INDEPENDIENTE donde Ho: SI HAY INDEPENDENCIA
H1: NO INDEPENDENCIA
Mi hipótesis de independencia, es aquella que me dice que si hay independencia, esto dependiendo del caso que corresponde al ejercicio en el paso 5.
Realizamos dos ejercicios durante la clase del seminario del dís de hoy, algo que no me quedo muy claro la sesión pasada fue el paso numéro 6, en el que identifico mi hipótesis independiente, ya que me resultaba confuso.
Lo que entendi el día de hoy acerca de este punto, es que debo saber cual de las dos hipótesis es la independiente, si la ALTERNATIVA o la NULA, mediante los sig. pasos:
CASO 1 Hinv: INDEPENDIENTE donde Ho: NO HAY INDEPENDENCIA
H1: SI HAY INDEPENDENCIA
CASO 2 Hinv: NO INDEPENDIENTE donde Ho: SI HAY INDEPENDENCIA
H1: NO INDEPENDENCIA
Mi hipótesis de independencia, es aquella que me dice que si hay independencia, esto dependiendo del caso que corresponde al ejercicio en el paso 5.
08/03/2012
Hoy en mi seminario de estadística aplicada abordamos el tema de PRUEBA DE INDEPENDENCIA Y HOMOGENEIDAD PARA RANGOS, este tema nos ayudará a obtener valores de variables categoricas que son independientes, es decir, a determinar si entre una variable y otra existe independencia o no. nos permite medir las relaciones entre variables.
Al igual que en las pruebas vistas hsta el momento, usaremos un porcentaje de confiabilidad, solo que en esta prueba haremos uso de las TABLAS DE CONTINGENCIA.
Realizaremos nuetros ejercicios basandonos en 7 pasos específicos que son:
1.- IDENTIFICAR LA HIPÓTESIS. Aqui anotaremos nuestra hipótesis textual, es decir la hipótesis de investigación.
2.-OBTENER EL VALOR CRÍTICO DE CHI CUADRADO. Obtendremos un valor crítico haciendo uso de los grados de libertad obtenidos con la operacion (F-1 (C-1), y del valor de ALFA.
3.-EXAMINAR LOS VALORES ESPERADOS PARA CADA CELDA. Dentro de este paso realizaremos otra tabla de contingencia en la que obtendremos valores diferentes al dividir el total de una variable perteneciente a una columna entre el total de casos y multiplicarlo por el total de una fila. Este procedimiento debe realizarse con cada uno de los valores para completar esta segunda tabla.
4.-OBTENER EL VALOR DEL ESTADÍSTICO DE PRUEBA DE INDEPENDENCIA. Lo cual se lograra con la sig. formula ∑ (oi-ei)/ ei, donde oi siempre representara cada uno de los valores de la tabla 1, y ei representara cada valor de la tabla 2.
Al final se sumaran todos los resultados obtenidos de mis tablas, al aplicar la formula.
5.- IDENTIFICAR EL TIPO DE CASO. Para lo que existen dos tipos de caso aue son:
CASO 1 Hinv: INDEPENDIENTE
CASO 2 Hinv: NO INDEPENDIENTE
Dentro de este mismo paso aplicaremos la decision estadística para rechazar o no la hipótesis mediante el siguiente criterio:
Si el valor estadístico es mayor al valor crítico, concluimos que debemos rechazar la hipótesis.
6.- IDENTIFICAR MI HIPÓTESIS INDEPENDIENTE. En este paso reconoceremos nuestra hipótesis independiente haciendo uso de los tipos de caso sabre si la hipótesis alternativa es INDEPENDIENTE O NO ya que es la que apoya mi hipótesis de investigación.
7.-INTERPRETACION DE LOS DATOS. Por último elaboraremos nuestra interpretacion de los datos.
Hoy en mi seminario de estadística aplicada abordamos el tema de PRUEBA DE INDEPENDENCIA Y HOMOGENEIDAD PARA RANGOS, este tema nos ayudará a obtener valores de variables categoricas que son independientes, es decir, a determinar si entre una variable y otra existe independencia o no. nos permite medir las relaciones entre variables.
Al igual que en las pruebas vistas hsta el momento, usaremos un porcentaje de confiabilidad, solo que en esta prueba haremos uso de las TABLAS DE CONTINGENCIA.
Realizaremos nuetros ejercicios basandonos en 7 pasos específicos que son:
1.- IDENTIFICAR LA HIPÓTESIS. Aqui anotaremos nuestra hipótesis textual, es decir la hipótesis de investigación.
2.-OBTENER EL VALOR CRÍTICO DE CHI CUADRADO. Obtendremos un valor crítico haciendo uso de los grados de libertad obtenidos con la operacion (F-1 (C-1), y del valor de ALFA.
3.-EXAMINAR LOS VALORES ESPERADOS PARA CADA CELDA. Dentro de este paso realizaremos otra tabla de contingencia en la que obtendremos valores diferentes al dividir el total de una variable perteneciente a una columna entre el total de casos y multiplicarlo por el total de una fila. Este procedimiento debe realizarse con cada uno de los valores para completar esta segunda tabla.
4.-OBTENER EL VALOR DEL ESTADÍSTICO DE PRUEBA DE INDEPENDENCIA. Lo cual se lograra con la sig. formula ∑ (oi-ei)/ ei, donde oi siempre representara cada uno de los valores de la tabla 1, y ei representara cada valor de la tabla 2.
Al final se sumaran todos los resultados obtenidos de mis tablas, al aplicar la formula.
5.- IDENTIFICAR EL TIPO DE CASO. Para lo que existen dos tipos de caso aue son:
CASO 1 Hinv: INDEPENDIENTE
CASO 2 Hinv: NO INDEPENDIENTE
Dentro de este mismo paso aplicaremos la decision estadística para rechazar o no la hipótesis mediante el siguiente criterio:
Si el valor estadístico es mayor al valor crítico, concluimos que debemos rechazar la hipótesis.
6.- IDENTIFICAR MI HIPÓTESIS INDEPENDIENTE. En este paso reconoceremos nuestra hipótesis independiente haciendo uso de los tipos de caso sabre si la hipótesis alternativa es INDEPENDIENTE O NO ya que es la que apoya mi hipótesis de investigación.
7.-INTERPRETACION DE LOS DATOS. Por último elaboraremos nuestra interpretacion de los datos.
martes, 6 de marzo de 2012
06/03/2012
El dìa de hoy el profesor de nuestro seminario de estadìstica aplicada nos indico que daba inicio el seminario como tal, es decir a partir de esta tercera unidad trabajariamos con el sistema de un seminario como meramente debe ser.
Terminamos la unidad I y II, e iniciaremos la III con las pruebas de independencia , homogeneidad, y otras como Wilconxon y la de Sperman, las cuales nos ayudaran a trabajar con datos que No se encuentran distribuidos normalmemte y por lo mismo no pueden representarse en una gràfica de Gausse.
Este tipo mde pruebas tambien es recomendable para trabgajar con muestras pequeñas.
La prueba de independencia, por ejemplo, nos permite determinar si existe o no dependencia entre dos factores o variables categòricas, tambièn es aplicable a las variables numèricas.
Respecto a otro punto, algunos compañeros comentan que no entienden la clase, asi que se acordo otra manera de llevarla a cabo por el profesor.
Considero que no pueden esperar a que el profesor adivinine quien tiene dudas y quien no pues es un error el no exponer las dudas que se presenten a lo largo de las clases.
El dìa de hoy el profesor de nuestro seminario de estadìstica aplicada nos indico que daba inicio el seminario como tal, es decir a partir de esta tercera unidad trabajariamos con el sistema de un seminario como meramente debe ser.
Terminamos la unidad I y II, e iniciaremos la III con las pruebas de independencia , homogeneidad, y otras como Wilconxon y la de Sperman, las cuales nos ayudaran a trabajar con datos que No se encuentran distribuidos normalmemte y por lo mismo no pueden representarse en una gràfica de Gausse.
Este tipo mde pruebas tambien es recomendable para trabgajar con muestras pequeñas.
La prueba de independencia, por ejemplo, nos permite determinar si existe o no dependencia entre dos factores o variables categòricas, tambièn es aplicable a las variables numèricas.
Respecto a otro punto, algunos compañeros comentan que no entienden la clase, asi que se acordo otra manera de llevarla a cabo por el profesor.
Considero que no pueden esperar a que el profesor adivinine quien tiene dudas y quien no pues es un error el no exponer las dudas que se presenten a lo largo de las clases.
sábado, 3 de marzo de 2012
02/03/2012
¿CÓMO INGRESAR DATOS EN EXCEL PARA UNA MEDIA, DOS MEDIAS, UNA PROPORCIÓN Y DOS PORPORCIONES?
La hoja de cálculo de excel nos permite ingresar formulas para obtener datos como: ESTADÍSTICO DE PRUEBA, ESTIMACIÓN MANCOMUNADA, TOTALES, ETC.
La fórmula para medias poblacionales y proporciones poblacionales se puede realizar primero desde Word para después copiarla a la hoja de calculo, ya que desde esta no0 es posible.
Al ingresar la formula en excel para obtener el estadistico de prueba o la estimacion mancomunada, se debe escribir la palabra RAIZ completa y posteriormenente la formula como se indica, ya que el signo de raiz no aparece en excel, el signo de multiplicacion se representa con el asterisco.
Automaticamente al cambiar los datos anotados en cada celda, el total o promedio obtenido va modificandose.
¿CÓMO INGRESAR DATOS EN EXCEL PARA UNA MEDIA, DOS MEDIAS, UNA PROPORCIÓN Y DOS PORPORCIONES?
La fórmula para medias poblacionales y proporciones poblacionales se puede realizar primero desde Word para después copiarla a la hoja de calculo, ya que desde esta no0 es posible.
Al ingresar la formula en excel para obtener el estadistico de prueba o la estimacion mancomunada, se debe escribir la palabra RAIZ completa y posteriormenente la formula como se indica, ya que el signo de raiz no aparece en excel, el signo de multiplicacion se representa con el asterisco.
Automaticamente al cambiar los datos anotados en cada celda, el total o promedio obtenido va modificandose.
jueves, 1 de marzo de 2012
01/03/2012
El pasado dìa martes 28 de febrero presentamos el primer examen de nuestro seminario de estadìstica del 4º semestre, en este examen aplicamos los conocimientos adquiridos respecto a la elaboraciòn de hipòtesis de investigaciòn, el estadìstico de prueba, el juicio de valor, las pruebas de hipòtesis para medias y proporciones, etc.
Hoy repasamos el examen y lo resolvimos juntos en clase con el apoyo del profesor, y de esto recupere lo soguiente:
Lo antriornos indica una proporcion , es decir, que del total, que son 225, se tomo una parte que corresponde a 97, y esto se manejaria en fraccion de esta manera 97/225.
Por otro lado, cuando se habla de muestras, nos damos cuenta porque maneja el dato del promedio o medIA, QUE ES UN ELEMENTO INDISPENSABLE para obtener el estadìstico de prueba.
Dentro de las pruebas de hipòtesis para dos medias poblacionales, se manejan dos diferentes promedios, que son X1 y X2,donde X1 representa la media muestraol del investigador, y X2 representa la media muestral establecida anteriormente a la investigacion del investigador.
Dentro de las proporciones, tambien se establecen son valores diferentes, que son:
P que se refiere al dato del investigador y Po, que representa los datos establecidos anteriormente.
El pasado dìa martes 28 de febrero presentamos el primer examen de nuestro seminario de estadìstica del 4º semestre, en este examen aplicamos los conocimientos adquiridos respecto a la elaboraciòn de hipòtesis de investigaciòn, el estadìstico de prueba, el juicio de valor, las pruebas de hipòtesis para medias y proporciones, etc.
Hoy repasamos el examen y lo resolvimos juntos en clase con el apoyo del profesor, y de esto recupere lo soguiente:
- Utilizamos la regla t- student y la regla para el valor de Z.
- Debemos utilizar la prueba de hipòtesis para proporciones cuando se nos habla, como lo indica su nombre de proporciones, o cuando se hace mencion del porcentaje. Como por ejemplo:
Lo antriornos indica una proporcion , es decir, que del total, que son 225, se tomo una parte que corresponde a 97, y esto se manejaria en fraccion de esta manera 97/225.
Por otro lado, cuando se habla de muestras, nos damos cuenta porque maneja el dato del promedio o medIA, QUE ES UN ELEMENTO INDISPENSABLE para obtener el estadìstico de prueba.
Dentro de las pruebas de hipòtesis para dos medias poblacionales, se manejan dos diferentes promedios, que son X1 y X2,donde X1 representa la media muestraol del investigador, y X2 representa la media muestral establecida anteriormente a la investigacion del investigador.
Dentro de las proporciones, tambien se establecen son valores diferentes, que son:
P que se refiere al dato del investigador y Po, que representa los datos establecidos anteriormente.
Suscribirse a:
Entradas (Atom)