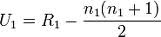7/06/2012

Mi aprendizaje el día de hoy es que en la prueba de U Mann Whitney no es posible trabajar con variables categoricas, solo se trabaja con variables numericas y estas deben ser discretas, es decir, no se pueden manejar numeros decimales.

Es prueba nos permite saber si existe diferencia entre las variables, y para su aplicacion debemos asignar lugares a los datos obtenidos, es decir, se trabajara con rangos.

Acudiremos a una escuela primaria el dia de mañana para aplicar un cuestionario a los alumnos, y se trabajara con sus promedios obtenidos el primero, segundo y tercer bimestre en la asignatura de matemáticas, para determinar finalmente si existe diferencia en el promedio de niños que usan el libro de texto gratuito de esta materia y los que no lo usan.

5/06/2010

ELABORACION DE INSTRUMENTOS

Ya tenemos el marco teorico, ahora debemos elaborar el instrumento que nos servira para recabar la informacion que requerimos.

La idea es esta:

Se desea comprobar si existe diferencia en el aprovechamiento de los niños de cuarto año de nivel primaria que aprenden las matematicas con el libro de texto, y los niños que no lo utilizan para aprender las matemáticas.

Para lo anterior se tomaran dos muestras independientes de 20 alumnos cada una. En una de las muestras los alumnos utilizan el libro de texto para aprender matematicas, y en la otra muestra no lo utilizan.

Si mis muestras son de la misma poblacion es necesario realizar antes la prueba de independencia, si mis muestras pertenecen a dos poblaciones distintas no es necesario aplicar la prueba de independencia debido a que la prueba que aplicaremos es la de U MANN WHITNEY, y esta se utiliza para muestras independientes, con variables numericas discretas. Estos son los requisitos para su aplicación.

1/06/2012

MARCO TEÓRICO

El marco teorico dentro de nuestro trabajo nos permitira conocer los resultados obtenidos en investigaciones anteriores, es decir, nos servirá de guía para tener una idea más clara de los diferentes procedimientos empleados para realizar una investigación similar a nuestro tema que es:

¿EL USO DE LOS LIBROS DE TEXTO DE MATEMÁTICAS INFLUYE EN EL APROVECHAMIENTO ESCOLAR?

31/05/2012

INICIAMOS CON LA ELABORACIÓN DE NUESTRO TRABAJO DE INVESTIGACIÓN

Hoy dio inicio la elaboracion del trabajo de investigacion en el cual aplicaremos nuestros conocimientos acerca de lo aprendido en el seminario.

Se elaborará una idea de investigación para que apartir de esto se trabaje con datos recolectados, utilizando instrumentos, y posteriormente se aplique la prueba que nos permita aceptar o anular nuestra hipótesis de investigación.

29/05/2012

EXPOSICIÒN 4ta. UNIDAD EN EL SEMINARIO DE ESTADISTICA INFERENCIAL

El dia de hoy se llevo a cabo la exposicion dentro del SEminario de Estadistica Inferencial Aplicada a la Investigaciòn Educativa, esto me permitio reforzar mis conocimientos en relacion a las ultimas 5 tipos de pruebas vistas en clase, que fueron: CORRELACION DE SPEARMAN, T DE DIFERENCIAS, U MANN DE WHITNEY, H DE KURSKAL WALLIS Y TUKEY.

Todas estas pruebas me seran de gran utilidad al momento de realizar mi trabajo de investigacion, no solo de esta materia, sino de todas las demas, asi como al momento de realizar mi trabajo de investigacion para la elaboracion de mi tesis de titulacion.

Una de las pruebas que mas se me dificulto fue la H de Kurskal Wallis debido a lo extenso del procedimiento, pues se trabaja con mas de dos variables al mismo tiempo, sin embargo el dia de hoy gracias a las exposiciones, me fue posible comprender mejor el procedimiento de esta prueba.

25/05/2012

EL DIA DE HOY DURANTE MI EXAMEN EN EL SEMINARIO DE ESTADISTICA APRENDI QUE EL VALOR DE ALFA ES LO MISMO QUE EL NIVEL DE SIGNIFICANCIA, SOLO QUE DEBO CONVERTIR A DECIMALES DE 1, ES DECIR EL 5% DE SIGNIFICANCIA EQUIVALE A .05% DEL VALOR DE ALFA.

ESTO ES MUY IMPORTANTE AL MOMENTO DE BUSCAR MI VALOR EN LAS TABLAS PARA LOCALIZAR EL ESTADISTICO DE PRUEBA Y SABER SI SE RECHAZA O NO LA Ho

24/05/2012

Una ventaja de la prueba Tukey es que mantiene el nivel del error tipo I (es decir, encontrar una diferencia cuando ninguna existe) que es igual a elegir el nivel alfa (es decir, α=.05 o α=.01). Una ventaja adicional de la prueba Tukey es que permite el cálculo de intervalos de confianza para las diferencias entre las medias.


Mi aprendizaje el día de hoy durante mi seminario de estadística fue que DMS Tukey es el estadístico de prueba que se deberá encontrar.


Y para tomar la decision estadística se procederá de la sig. forma:


-Si DMS es superior a CMd, se dice que hay una diferencia significativa entre las medias comparadas, si estro sucede se debe averiguar cual de las medias comparadas posee una mayor diferencia en comparacion con la media de las diferencias evaluadas.


Al aplicar la fórmula `para obtener el estadístico de prueba, se debe considerar, al sustituir, a Xi como el valor mas grande, y a Xj, como el valor mas pequeño, y a cada una de estas corresponde nj (Xj), y ni (Xi).

22/05/2012

PRUEBA TUKEY

La prueba Tukey se usa en experimentos que implican un número elevado de comparaciones o se desea usar una prueba más rigurosa que la de Duncan.

Es de fácil cálculo puesto que se define un solo comparador, resultante del producto del error estándar de la media por el valor tabular en la tabla de Tukey usando como numerador el número de tratamientos y como denominador los grados de libertad del error.

De esta manera, aplicando los datos del ejemplo de Duncan, tendríamos que el dato de la tabla para 5 tratamientos y 8 grados de libertad es 4.89, que multiplicado por el error estándar (0.122) nos da 0.59.

Por lo consiguiente, en este ejemplo sólo los tratamientos B y E presentan una diferencia significativa.

Tenemos entonces que si por lo menos dos medias difieren entre si, pero no se sabe cuales son, con esta prueba sabremos que parejas de medias son significativamente distintas entre sì.

Mi aprendizaje el dìa hoy fue significativo porque esta prueba es otra opcion junto con la de t student, solo que a diferencia de esta ùltima, la prueba de TUKEY nos permite obtener la diferencia de las medias que se combinan entre sì.

18/05/2012

HOY DURANTE MI SEMINARIO DE ESTADÍSTICA INFERENCIAL, aprendi que para obtener los grados de libertad en esta prueba debo restar 1 al total de columnas con que se esta trabajando, tambien aprendi que al momento de graficar los valores obtenidos de Rc al cuadrado, esto no repervute en mi interpretacion de los datos, pues lo que realmente cuenta es el resultado de la gráfica al momento de ubicar el valor de H, pues de esta forma es que sabre si la Ho se acepta o se rechaza.

Deseo mostrar un ejemplo de esta prueba para una mejor comprension del tema.

Un investigador estudia el efecto benéfico de cuatro sustancias anticonvulsionantes (fenobarbital, difenilhidantoinato -DFH-, diacepam y clonacepam), para proteger contra la muerte producida por un convulsionante, la tiosemicarbazida, la cual se manifiesta después de crisis clónica y tónica, respectivamente. El investigador elige al azar a 24 ratones de la misma edad y peso y les inyecta anticonvulsionante previamente a la tiosemicarbazida. A partir de este momento, inicia la cuenta en tiempo, hasta que mueren los ratones; además mide las observaciones en horas de tiempo transcurrido.

Elección de la prueba estadística.
Las mediciones se realizan en horas, por lo que la variable puede ser continua y, en consecuencia, una escala de intervalo; sin embargo, algunos ratones no murieron y el tiempo está calificado nominalmente como infinito. Este obstáculo impide concederle la calificación de escala de intervalo, por lo cual se elige una escala de tipo ordinal. Véase: Estadística/Flujogramas/Flujograma 4

Planteamiento de la hipótesis.

• Hipótesis alterna (Ha). La protección de la muerte por drogas anticonvulsionante contra el fármaco convulsionante tiosemicarbazida, se muestra diferente entre los cuatro grupos, y hay mejor protección por el diacepam.
• Hipótesis nula (Ho). Las diferencias observadas en los cuatro grupos de fármacos anticonvulsionantes, para evitar la muerte producida por la tiosemicarbazida, se deben al azar.

Nivel de significación.
Para todo valor de probabilidad igual o menor que 0.05, se acepta Ha y se rechaza Ho.

Zona de rechazo.
Para todo valor de probabilidad mayor que 0.05, se acepta Ho y se rechaza Ha.

Tiempo en horas que tarda el fármaco en causar la muerte en ratones.

Aplicación de la prueba estadística.
De acuerdo con los pasos, se inicia con el ordenamiento de todas las observaciones a partir del valor más pequeño hasta el mayor y la detección de las ligas o empates.
Arreglo de los datos para asignar rangos y detectar las ligas o empates.

Una vez efectuado el ordenamiento en rangos de las observaciones, se hacen las sumatorias de los rangos. Para facilitar esta tarea, elabórese una tabla en la que sustituyan los datos.

Sustitución por rangos. Observaciones de la primera tabla.

Se calcula el valor de ajuste por ligas con la siguiente fórmula:

Con el ajuste de L, se procede a calcular el valor estadístico de la prueba de Kruskal-Wallis.

Calculamos los grados de libertad.

gl = K grupos - 1 = 4 - 1 = 3

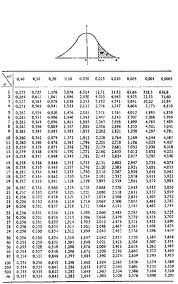
El estadístico H calculado de 15.4, se compara con los valores críticos de ji cuadrada. En seguida se busca en esa hilera la cifra de grados de libertad (3) hasta el nivel de significancia de 0.05 y se observa el valor 7.82, hasta los críticos 11.34 y 16.27, donde se encuentra el calculado. Esto quiere decir que la probabilidad de que exista una diferencia se halla a una probabilidad de error entre 0.01 y 0.001.

Decisión.
Como el valor estadístico H tiene una probabilidad menor que 0.01 y éste es menor que el nivel de significancia, se acepta Ha y se rechaza Ho.

Interpretación.
Entre las drogas anticonvulsionantes, existe diferencia significativa en cuanto a la protección de muerte a los ratones cuando se les inyecta el fármaco tiosemicarbazida. El diacepam se manifestó principalmente con los rangos más altos y se muestra distinto de los demás anticonvulsionantes (véase la siguiente figura).

Sumatoria de rangos de las observaciones.

17/05/2012

PRUEBA H DE KRUSKAL WALLIS

La prueba de Kruskal-Wallis fue propuesta por William Henry Kruskal (1919- ) y W. Allen Wallis (1912-1998) en el artículo "Use of ranks in one-criterion variance analysis" publicado en el “Journal of American Statistics Association” en 1952.

Cuando el análisis de la varianza no es aplicable debido a incumplimientos de las suposiciones del modelo,
es necesario aplicar la prueba de Kruskal-Wallis para el contraste de k medianas. Esta prueba es una
ampliación de la prueba de Mann-Whitney-Wilcoxon para dos medianas, en razón de que se usan rangos para su aplicación; por otra parte, este procedimiento se emplea cuando el modelo experimental contiene más de dos muestras independientes.

Dicha prueba se define matemáticamente de la forma siguiente:

Donde: H = valor estadístico de la prueba de Kruskal-Wallis. N = tamaño total de la muestra. Rc2 = sumatoria de los rangos elevados al cuadrado. ni = tamaño de la muestra de cada grupo. L = ajuste dado por el ajuste de ligas o empates de los rangos.

El ajuste L se calcula de la manera siguiente:

Donde: Li = valor de número de empates de un rango. N = tamaño total de la muestra.

Se utiliza cuando:

• Cuando son diferentes tratamientos o condiciones.
• Muestras pequeñas.
• Se utiliza escala ordinal.
• Si las muestras se seleccionaron de las diferentes poblaciones.
• Contrastar hipótesis (direccional o no direccional)

PARA APLICAR ESTA FÒRMULA SE DEBERÀ PROCEDER DE LA SIG. FORMA:

1. Ordenar las observaciones en rangos de todos los grupos, del más pequeño al mayor.
2. Asignar el rango para cada observación en función de cada grupo de contraste, elabora la sumatoria de rangos, elevar al cuadrado este valor y dividirlo entre el número de elementos que contiene (ni).
3. Detectar las ligas o empates entre los rangos de cada grupo y aplicar la ecuación (L) para obtener el ajuste.
4. Aplicar la ecuación de Kruskal-Wallis y obtener el estadístico H.
5. Calcular los rangos de libertad (gl): gl = K grupos - 1.
6. Comparar el estadístico H, de acuerdo con los grados de libertad, en la tabla de distribución de ji cuadrada en razón de distribuirse de forma similar.
7. Decidir si se acepta o rechaza la hipótesis.

Es importante mencionar que para aplicar la fòirmula de Li, debo solamente saber cuantas veces se empata cada valor, tomando en cuenta solo los que se empataron, y posteriormente debo asignar un lugar columna por columna a cada uno de los valores, esto para obtener el total de Rc.

11/05/2012

En la prueba de U MANN WHITNEY, al momento de otorgar un lugar a los valores de cada una de las columnas, SI EXISTE EMPATE entre estos, se deberan sumar las posiciones de estos valores repetidos y a continuacion dividirlos entre el total de valores que se repiten. EJEMPLO:
1º  24
2º  36
3º  36
4º  36
5º   66
6º  94

SE PROCEDE DE LA SIG. MANERA:

2+3+4= 9 / 3= 3

Y entonces el numero 3º sera la posiciòn que ocupara cada uno de los valores que se repiten.

10/05/2012

AL UTILIZAR LA PRUEBA DE U MANN-WHITNEY, PRIMERO SE DEBE ELABORAR LA HIPOTESIS TEXTUAL, DESPUES SE PROCEDE A ORDENAR LOS DATOS DE LAS COLUMNAS DEL MENOR AL MAYOR DE LOS VALORES, SIN IMPORTAR SI SE DEBEN INTERCALAR LAS COLUMNAS. POR EJEMPLO:

COLUMNA A                      COLUMNA B
95                                                  80
100                                                85
93                                                  25
110                                                 70
45                                                  90

SE LES ASIGNA UN LUGAR DE LA SIG. FORMA:

1º   25
2º   45
3º   70
4º   80
5º   85
6º   90
7º   93
8º   95
9º   100
10º  110

DESPUES DE EL PASO ANTERIOR SE SUMAN LOS LUGARES DE CADA COLUMNA POR SEPARADO, ES DECIR DE LA COLUMNA A, Y DE LA COLUMNA B. ASI SE OBTIENE LA SUMATORIA TOTAL DE LOS RANGOS 1 Y 2. POR EJEMPLO:
8º+9º+7º+10º+2º= 36
4º+5º+1º+3º+6º= 19

AL CONCLUIR LOS PASOS ANTERIORES ES POSIBLE APLICAR LA FORMULA PARA OBTENER EL RESULTADO TANTO DE U1, COMO DE U2.

07/05/2012

PRUEBA U MANN- WHITNEY

La alternativa no paramétrica para el contraste de dos muestras independientes es la prueba U de Mann-Whitney.

Esta prueba estadística es útil cuando las mediciones se pueden ordenar en escala ordinal (es decir, cuando los valores tienden a una variable continua, pero no tienen una distribución normal) y resulta aplicable cuando las muestras son independientes.

Este procedimiento es una buena alternativa cuando no se puede utilizar la prueba t de Student, en razón de no cumplir con los requisitos que esta prueba exige.

La fórmula es la siguiente:

donde n₁ y n₂ son los tamaños respectivos

Donde:
U₁ y U₂ = valores estadísticos de U Mann-Whitney.
n₁ = tamaño de la muestra del grupo 1.
n₂ = tamaño de la muestra del grupo 2.
R₁ = sumatoria de los rangos del grupo 1.
R₂ = sumatoria de los rangos del grupo 2.

Pasos:

1. Determinar el tamaño de las muestras (n₁ y n₂). Si n₁ y n₂ son menores que 20, se consideran muestras pequeñas, pero si son mayores que 20, se consideran muestras grandes.
2. Arreglar los datos en rangos del menor al mayor valor. En caso de que existan ligas o empates de rangos iguales, se deberán detectar para un ajuste posterior.
3. Calcular los valores de U₁ y U₂, de modo que se elija el más pequeño para comparar con los críticos de U Mann-Whitney de la tabla de probabilidades asociadas con valores pequeños como los de U en la prueba de Mann-Whitney.
4. En caso de muestras grandes, calcular el valor Z, pues en estas condiciones se distribuye normalmente.
5. Decidir si se acepta o rechaza la hipótesis.

04/05/2012

Prueba t  La prueba t es un método estadístico para determinar si la diferencia observada entre dos medias (promedios) muestrales se puede atribuir al azar o si en realidad la diferencia es estadísticamente significativa. Dos tipos de pruebas Independiente y pareada .

 Prueba para datos independientes Evalúa las diferencias entre dos grupos independientes  Ejemplo El promedio del peso de un grupo de hombres Versus El promedio del peso de un grupo de mujeres
 Grados de libertad: n1 + n2 – 2  Establecer el nivel de significancia (usualmente 0.05 o 5% de error o 95% de confianza)

Si estamos comparando un resultado cuantitativo en dos grupos de datos, a partir de muestras extraídas de forma aleatoria de una población normal, siendo n_A el tamaño de la primera muestra y n_B el de la segunda, ES POSIBLE TOMAR LA SIG. FÓRMULA
:

03/05/2012

El día de hoy tomamos el tema de PRUEBA "T" DE DIFERENCIAS

En esta prueba se requiere hacer uso de la tabla "t" student que utilizamos en temas anteriores, en este caso para obtener el estadístico de prueba se debe obtener la VARIANZA  (S2) ya que en la fórmula de esta prueba se requiere de este dato.

Los pasos son muy sencillos:

1.- OBTENER LAS HIPÓTESIS
2.- OBTENER EL VALOR DE LA VARIANZA
3.-OBTENER EL ESTADÍSTICO DE PRUEBA CON LA FÓRMULA ESPECÍFICA PARA ELLO
4,.- OBTENER LOS GRADOS DE LIBERTAD CON LA FÓRMULA: n1+n2-2= Y PROCEDER A BUSCAR EL VALOR EN LA TABLA T-STUDENT

5.- LA INTERPRETACIÓN DE LOS DATOS

26/04/2012

PRUEBA DE CORRELACION DE PEARSON.

Para obtener el nùmero promedio de ciertos datos, en esta prueba, se debe sustituir en la fòrmula los resultados obntenidos de a y b respectivamente y  tomando como el valor de X los lìmites tanto inferiores como superiores, se procede a sustituir.

Por ejemplo:
Si en algùno de los problemas mis resultados de a,b y r son los siguientes:

a= 6.4091
b=0.000442

y mis lìmites de datos son los siguientes:

dato inferior= 0.01
dato superior= 7.96

Procedo a sustituir en la fòrmula de la siguinte manera:

y= 6.4091+0.000442 (0.01)=

y=6.4091+0.0004420(7.96)=

De esta forma obtengo el NÙMERO PROMEDIO de determinados datos.

24/04/2012

Al sustituir en la fòrmula   para la correlaciòn se debe tomar en cuenta que siempre se tomarà como X el dato que se nos proporcione, y como Y el dato que se desea encontrar.
Al realizar predicciones en esta prueba, siempre se tomara en cuenta el rango de valores que poseen nuestros dattos, es decir, el valor menor y el valor mayor. Nuestro resultado debe estar dentro de este rango de valores para que sea vàlido y se pueda continuar con la investigaciòn, ya que aunque matemàticamente el resultado sea correcto, estad÷isticamente no serà vàlido.

En esta imagen se muestra graficamente que entre mas unidos esten los puntos mayor es la correlacion entre los datos,  y por el contrario, mientras màs dispersos menor correlaciòn existe.

20/04/2012

El dìa de hoy en el seminario de estadìstica inferencial aplicada a la investigacion educativa, recordamos el tema de correlacion lineal que vimos el semestre anterior.

Ahora podremos aplicar este mètodo como prueba para saber si ecxiste relacion o no entre las variables del tipo continuas, esto es utilizando cantidades con decimal.

Deseo mencionar como dato importante, para mi, que si se obtiene una correlacion de 1(100%), tendremos una correlacion perfecta, por lo mismo, si tenemos una correlacion alta, tendremos una relacion alta.

CORRELACION LINEAL

La fòrmula para obtener la correlacion de las variables es:   y= a+bx

NUBE DE PUNTOS

en la siguientes imagenes se muestras algunosa tipos de nube de puntos obtenida al graficar los datos para determinar una correlacion.

                                                                                       

17/04/2012

Mi aprendizaje el dìa de hoy fue que el determinar que cola se usara en la prueba de homogeneidad, si la izquierda o la derecha, es fundamental ya que esto altera totalmente mi interpretacion de los datos, asi como mi decision estadìstica.

Debo ser totalmente cuidadosa de ahora en adelante de este aspecto al usar los diferentes mètodos, ya que en mi examen esto repercutio considerablemente pues la calificaciòn obtenida fue muy baja.

Para determinar las colas que elegire debo basarme en el tipo de caso que es el siguiente:

CASO 1    Hinv: SI hay homogeneidad

CASO 2:  H1: NO hay homogeneidad

Tambièn aprendì que en la prueba de hipòtesis para una media poblacional, debo considerar a la hipòtesis de investigaciòn como mi media poblacional para determinar si usare la cola del lado derecho o del lado izquierdo.

Por ùltimo un aprendizaje de significancia el dìa de hoy en mi seminario de investigaciòn es que confirme que las apariencias engañan, y que debemos cuidar lo que hablamos y con quien pues se pueden presentar muchos malos entendidos por confiar equivocadamente.

29/03/2012

CASOS AJUSTADOS MAYORES A 15. para este tipo de casos, dentro de la prueba de Wilcoxon  se debe obtener la diferencia de rangos por medio de las tres formulas que me permitan obtener los valores de NTmas, sigmaT mas y el valor de Z al final, a partir del cual se aplicara la decision estadistica para saber si la hipotesis nula se rechaza o se acepta..

Es importante recordar que cuando se especifique que se debe trabajar con dos colas, el valor de alfa debe ser dividido entre dos, si solo se trabaja con una cola, el calor de alfa sera el mismo, es decir, que no cambiara.

Al momento de tomar la decision estadistica, se procedera de la siguiente manera:

Si el valor de Z  es mayor o igual al valor absoluto, la Ho se rechaza.
Es importante señalar tambien que la prueba de Wilcoxon se utiliza para diferencias proporcionales.

Si n es menor que 15 entonces hay que considerar el valor de alfa, si este es con una cola o con dos colas, porteriormente se obtiene una valor, el cual sera restado al valor que se obtenga de la tabla dos en sonde se toma en cuenta el valor de N corregido y el valor real de alfa. Lo que nos da como resultado un intervalo, al que realizaremos una operacion de resta, y al resultado obtenido le dividiremos entre el valor obtenido de la primer tabla en la que se considera si alfa trabaja con una cola o dos colas.

27/03/2012

EL APRENDIZAJE SIGNIFICATIVO PARA MI EL DÍA DE HOY FUÉ SOBRE LA PRUEBA DE WILCONXON PARA OBTENER LA DIFERENCIA DE RANGOS.

CUANDO SE TIENE EL VALOR DE ALFA, Y SE LLEGA AL PASO 5 PARA ENCONTRAR EL VALOR DE PROBABILIDAD, SE DEBE TENER COMO BASE LA TABLA QUE NOS SIRVE PARA ESTE CASO, LA CUAL ES LLAMADA VALOR DE PROBABILIDAD ASOCIADO A Tmas.

EL PRIMER PASO PARA OBTENER EL VALOR DE PROBABILIDAD ES OBTENER LOS SIGUIENTES VALORES:

n= TAMAÑO DE LA MUESTRA
N= VALOR DE N CORREGIDO

Y EL VALOR DE ALFA








UNA VEZ QUE SE OBTIENEN ESTOS VALORES, DEBO TOMAR MI PRIMER TABLA EN LA QUE UBICARÉ EL TAMAÑO DE MI POBLACIÓN, PRIMERO, Y POSTERIORMENTE DIVIDIRE ENTRE DOS EL VALOR DE ALFA,  ENCONTRANDO ASI LA UNIÓN ENTRE ESTOS DOS . Y ASÍ OBTENDRE UN PRIMER VALOR.

POSTERIORMENTE ME VOY A LA SEGUNDA TABLA Y UBICARÉ EN ESTA EL VALOR DE n CORREGIDA, ENCONTRANDO EL RESULTADO EN EL QUE SE UNA CON EL PORCENTAJE DE CONFIABILIDAD, LO CUAL ME DARÁ COMO RESULTADO UN INTERVALO, QUE SE EXPRESA A MANERA DE RESTA, REALIZARÉ LA OPERACIÓN Y EL RESULTADO OBTENIDO LO DIVIDIRÉ ENTRE EL VALOR QUE OBTUVE, ESTE SERÁ MI VALOR DE PROBABILIDAD, TAMBIÉN LLAMADO T  (mas).

ES POSIBLE ENCONTRAR UN TIPO DE GRÁFICA COMO LA SIGUIENTE:

23/03/2012

El día de hoy trabajamos con la prueba de Wilcoxon, la cual es una prueba de rangos asignados, que por no pertenecer a las pruebas NO PARAMËTRICAS, no requiiere de una distribución específica.

Se utiliza para comparar dos grupos relacionados de rangos, y para comparar que la diferencia sea estadísticamente significativa..

Los pasos a seguir para aplicar esta prueba son los siguientes:

1.-OBTENER LA DIFERENCIA DE RANGOS
2.-SELECCIONAR LOS RANGOS POSITIVOS Y LOS NEGATIVOS
3.-NUMERAR LOS RANGOS POSITIVOS Y LOS NEGATIVOS, Solo numerarlos no se deben ordenar
4.- OBTENER EL VALOR DE T mas y T menos.. Esto es el total de lugares que ocupan los valores positivos y los negativos.
5.-ENCONTRAR EL VALOR DE PROBABILIDAD SOCIADO A T(mas), CON EL NÚMERO AJUSTADO DE DATOS
6.- DECISIÓN ESTADÍSTICA

ALGUNAS DE LAS FÓRMULAS USADAS EN ESTA PRUEBA SON:

22/03/2012

El día de hoy se aplico la fórmula para la prueba de Sperman la cual como recordaremos es la siguiente:

Mediante el uso de esta formula sabremos si la correlacion existente entre las variables es baja o nula, media o moderada, u alta o grave.

Se debe proceder de la manera siguiente conforme a los pasos presentados a continuacion para aplicar dicha fórmula:

1.- Las variables deben ser ordenadas
2.- Una vez ordenadas las variables, se procede a obtener la prueba de diferencia de rangos.
3.- Construir una tabla de diferencia de rangos.
4.- En dado caso que las variables se empaten se debe aplicar la fórmula específicada para esto.
5.- Interpretacion de los datos.

Para los datos empatados se puede proceder de la sig. manera:

De las tablas que se elaboran, se debe obtener el cuadrado de la diferencia de cada uno de los lugares que ocupan las filas.

20/03/2012

PRUEBA DE CORRELACIÓN DE SPEARMAN  o  PRUEBAS DE LIBRE DISTRIBUCIÓN

Esta prueba es una alternativa al coeficiente de correlación lineal y a la correspondiente prueba "T",  la única condición que exige este método es que las variables sean por lo menos ORDINALES, es decir que se puedan ordenar.

Es importante señalar que dentro de la prueba de SPEARMAN, no es posible trabajar con variables nominales, esto debido a que no es posible ordenarlas.

por ejemplo:

Al trabajar con categorias como la edad, el nivel de estudios, el peso, la estatura, etc, es posoble aplicar esta prueba, ya que todas estas variables pueden ser ordenadas jerarquicamente.

En cambio al trabajar con variables nominales como el sexo, color favorito, etc, no es posible usar esta prueba, ya que las variables no llevan un orden.

Es importante mencionar que en esta prueba los datos no se encuentran distrubuidos normalmente, sino que son dispersos, en una gráfica quedarían representados más o menos así

La fórmula que se utiliza en esta prueba es la siguiente:

 

esta prueba nos permite obtener la PRUEBA DE DIFERENCIA DE RANGOS.

16/03/2012

PRUEBA DE HOMOGENEIDAD

Al interpretar mis datos con la prueba de homogeneidad, debo considerar que el proceso para determinar si rechazo o no mi Hinv. es el mismo que en la prueba de independencia, excepto que al señalar mis hipotesis en los tipos de caso, que son el CASO  1   y  el  CASO 2,  se establece si hay homogeneidad o no la hay . Es decir:

CASO  1    Hinv.   SI hay homogeneidad        
                   Ho:     NO hay homogeneidad
                   H1 :     SI  homogeneidad


CASO   2     Hinv:    NO hay homogeneidad
                     Ho:      SI  hay homogeneidad
                     H1:       NO  hay homogeneidad


De lo que se determinarà que:

Si  SI rechazo mi hipotesis de homogeneidad, SI habrà evidencia suficiente para sostener mi Hinv.

Por otra parte, si NO rechazo mi hipòtesis de homogeneidad, NO habrà evidencia suficiente para considerar mi Hinv.

Como podemos darnos cuenta, es en la interpretacion de los datos, donde mi HIPOTESIS CAMBIA, de nombrarse independiente, a nombrarse homogenea.

15/03/2012

MI APRENDIZAJE  el dìa de hoy surante el seminario de estadìstica aplicada a la investigaciòn educativa fue que la formula de YATES es muy ùtil y sencilla de usar, esto claro solo en los casos especiales en que se nos presenta una tabla con dos filas y con dos columnas.

De entrada parece una fòrmula complicada, por la extensiòn y sus componentes, pero al sustit6uir no es tan complicado como aparenta. Lo indispensable es sustituir bien las cantidades, y realizar las operaciones de manera adecuada para no caer en errores.

Por otra parte dio inicio el tema de PRUEBA DE HOMOGENEIDAD, la cual es una variante de la prueba de independencia, y se utiliza para comparar proporciones en las que ocurren los valores de una sola variable categòrica, en varias poblaciones distintas.

El procedimiento es el mismo que se aplica en la prueba de independencia, y se determinara que paso seguir para obtener el ESTADISTICO DE PRUEBA, dependiendo tambièn de cuantas filas y cuantas columnas tenemos.

13/03/2012

CORRECCIÓN DE YATES

Esta formula también es llamada CORREGIDA o SINTETIZADA, y es útil al encontrarnos con un caso especial en pruebas de independencia.

Estos casos especiales, se refieren a el encontrar una tabla que solo cuente con DOS FILAS, así como con DOS COLUMNAS, es decir, que al obtener los GRADOS DE LIBERTAD, estos nos den como resultado 1.
Un ejemplo de este tipo de tablas es la siguiente:


    CON DÉFICIT DE ATENCIÓN            SIN DÉFICIT DE ATENCIÓN                  TOTALES

M                        33                                                      112                                                145

H                       53                                                        201                                               254

TOTAL            86                                                         313                                                399


LA FÓRMULA QUE DEBEMOS UTILIZAR LLAMADA CORRECCIÓN DE YATES es la sig:

En esta fórmula solo debemos sustituir los datos que se presentan en nuestra tabla. Donde n, representa el total de datos , que en el caso de nuestra tabla anterior es 399.

09/03/2012

Realizamos dos ejercicios durante la clase del seminario del dís de hoy, algo que no me quedo muy claro la sesión pasada fue el paso numéro 6, en el que identifico mi hipótesis independiente, ya que me resultaba confuso.

Lo que entendi el día de hoy acerca de este punto, es que debo saber cual de las dos hipótesis es la independiente, si la ALTERNATIVA o la NULA, mediante los sig. pasos:

CASO 1   Hinv:  INDEPENDIENTE   donde    Ho: NO HAY INDEPENDENCIA
                                                                          H1: SI HAY INDEPENDENCIA

CASO  2  Hinv: NO INDEPENDIENTE  donde   Ho: SI HAY INDEPENDENCIA
                                                                              H1: NO INDEPENDENCIA

Mi hipótesis de independencia, es aquella que me dice que si hay independencia, esto dependiendo del caso que corresponde al ejercicio en el paso 5.

08/03/2012

Hoy en mi seminario de estadística aplicada abordamos el tema de PRUEBA DE INDEPENDENCIA Y HOMOGENEIDAD PARA RANGOS, este tema nos ayudará a obtener valores de variables categoricas que son independientes, es decir, a determinar si entre una variable y otra existe independencia o no. nos permite medir las relaciones entre variables.

Al igual que en las pruebas vistas hsta el momento, usaremos un porcentaje de confiabilidad, solo que en esta prueba haremos uso de las TABLAS DE CONTINGENCIA.

Realizaremos nuetros ejercicios basandonos en 7 pasos específicos que son:

1.- IDENTIFICAR LA HIPÓTESIS. Aqui anotaremos nuestra hipótesis textual, es decir la hipótesis de investigación.
2.-OBTENER EL VALOR CRÍTICO DE CHI CUADRADO. Obtendremos un valor crítico haciendo uso de los grados de libertad obtenidos con la operacion (F-1 (C-1), y del valor de ALFA.
3.-EXAMINAR LOS VALORES ESPERADOS PARA CADA CELDA. Dentro de este paso realizaremos otra tabla de contingencia en la que obtendremos valores diferentes al dividir el total de una variable perteneciente a una columna entre el total de casos y multiplicarlo por el total de una fila. Este procedimiento debe realizarse con cada uno de los valores para completar esta segunda tabla.
4.-OBTENER EL VALOR DEL ESTADÍSTICO DE PRUEBA DE INDEPENDENCIA. Lo cual se lograra con la sig. formula  ∑  (oi-ei)/ ei, donde   oi  siempre representara cada uno de los valores de la tabla 1, y ei representara cada valor de la tabla 2.
Al final se sumaran todos los resultados obtenidos de mis tablas, al aplicar la formula.
5.- IDENTIFICAR EL TIPO DE CASO. Para lo que existen dos tipos de caso aue son:
CASO  1    Hinv: INDEPENDIENTE
CASO 2     Hinv: NO INDEPENDIENTE
 Dentro de este mismo paso aplicaremos la decision estadística para rechazar o no la hipótesis mediante el siguiente criterio:
Si el valor estadístico es mayor al valor crítico, concluimos que debemos rechazar la hipótesis.
6.- IDENTIFICAR MI HIPÓTESIS INDEPENDIENTE. En este paso reconoceremos nuestra hipótesis independiente haciendo uso de los tipos de caso sabre si la hipótesis alternativa es INDEPENDIENTE O NO ya que es la que apoya mi hipótesis de investigación.
7.-INTERPRETACION DE LOS DATOS. Por último elaboraremos nuestra interpretacion de los datos.